UNIR Revista
El modelo CAPM es una fórmula que se utiliza para fijar el precio de un activo financiero, poniendo en relación la rentabilidad esperada del activo con el riesgo que implica.

El modelo CAPM (siglas de Capital Asset Pricing Model, que podemos traducir por modelo de fijación de precios de activos de capital) es un modelo de valoración de activos financieros que permite calcular la tasa de retorno de un activo financiero en función del riesgo asumido. Este modelo mide la relación entre el riesgo de invertir en un activo determinado y la rentabilidad esperada del mismo. Esta relación ayuda a fijar el precio de un activo financiero.
El modelo CAPM fue desarrollado por el economista estadounidense William Sharpe, que recibió el Premio Nobel de Economía en 1990 —junto a los también economistas Merton Miller y Harry Markowitz— por sus contribuciones a la teoría de la economía financiera.
El CAPM es un modelo teórico y, por tanto, parte de varias suposiciones. Así:
- Está basado en un entorno de equilibrio de mercado (la oferta de activos financieros es igual a la demanda, y la oferta es fija y conocida) y de competencia perfecta.
- Se asume que todos los inversores tienen aversión al riesgo y poseen la misma información.
- La rentabilidad de los activos se corresponde con una distribución normal.
- Solo se contempla el riesgo sistemático o de mercado, no así el riesgo específico de cada activo.
Pese a estas limitaciones, este modelo es muy utilizado por su facilidad y porque proporciona mucha información sobre cómo se comportan los activos.
Lo que concluye el modelo CAPM es que cuanto mayor es el riesgo que se asume, mayor es la rentabilidad esperada, por lo que si se pudiera medir exactamente el nivel de riesgo vinculado a un activo, se podría deducir el porcentaje exacto de rentabilidad potencial que ofrece este.
¿Cómo se calcula el modelo CAPM?
Siguiendo este razonamiento, el modelo CAPM desarrolla la siguiente fórmula para calcular la rentabilidad de un activo:
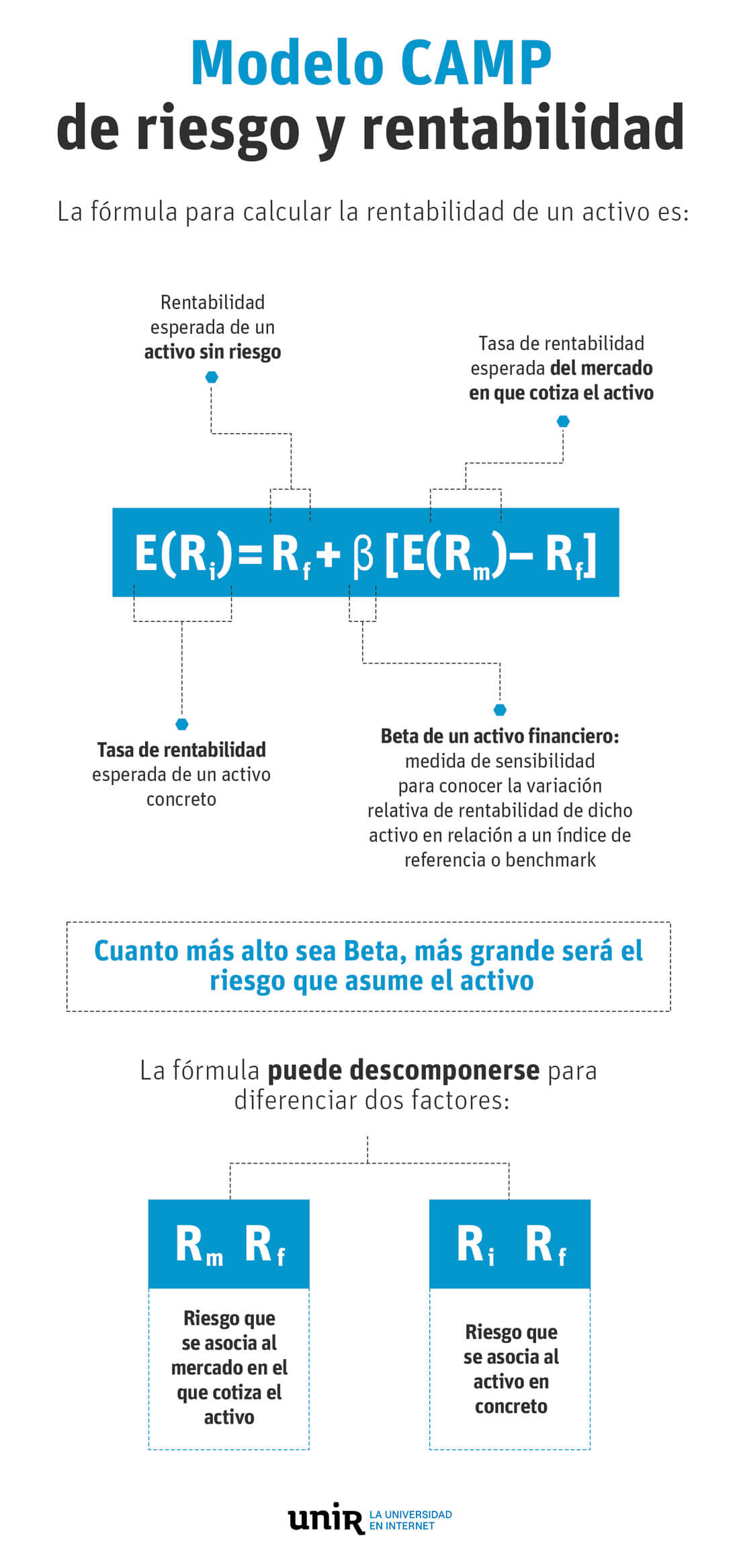
E(ri)= rf + β [E(rm)– rf]
Donde:
- E(ri): es la tasa de rentabilidad esperada de un activo concreto.
- rf: es la rentabilidad esperada de un activo sin riesgo.
- β o Beta: es una medida de sensibilidad que permite conocer la variación relativa de rentabilidad de un activo financiero en relación a un índice de referencia o benchmark. Normalmente este índice de referencia es el índice bursátil en el que cotiza el activo financiero.
- E(rm): es la tasa de rentabilidad esperada del mercado en que cotiza el activo.

Cuanto más alto sea Beta, más grande será el riesgo que asume el activo; es decir, que la rentabilidad esperada de un activo vendrá determinada por el valor de Beta, que sirve para medir el riesgo sistemático:
- Si Beta es mayor que 1, el activo tiene mayor riesgo que el mercado.
- Si Beta es inferior a 1, el activo tiene un riesgo menor que el mercado; es considerado, por tanto, de bajo riesgo.
- Si Beta es igual a 1, el riesgo del activo es similar al del mercado.
La fórmula puede descomponerse para diferenciar dos factores:
- rm – rf: es el riesgo que se asocia al mercado en el que cotiza el activo.
- ri – rf: es el riesgo que se asocia al activo en concreto.
El modelo CAPM en la práctica
Pongamos un ejemplo. Queremos calcular la tasa de rentabilidad de una acción de una empresa X que cotiza en el Ibex 35 .
Podemos considerar como ejemplo de un activo libre de riesgo las Letras del Tesoro a un año, cuya rentabilidad actual es del -0,465 %. Es decir que rf sería, para este ejemplo, igual a -0,465%.
La rentabilidad esperada para este año del Ibex 35 (el mercado en que cotiza el activo), E(rm)), es del 8 %.
Supongamos que la Beta de la acción en cuestión es de 1,1 respecto al Ibex 35, esto es, que las acciones de esta compañía oscilan un 10 % más de lo que lo hace el Ibex 35. Otra forma de expresarlo es decir que esas acciones tienen un 10 % más de riesgo sistemático.
Aplicando la fórmula del modelo CAPM:
- E(ri) = rf + β [E(rm)– rf]
- E(rx) = -0,00465 + 1,1 [0,08– (-0,00465) ]
- E(rx) = 8,8%
- Por tanto, según CAPM la rentabilidad esperada de la acción de la empresa X será del 8,8 %.
Fórmulas como la del modelo CAPM son de uso habitual en los departamentos financieros de las empresas para realizar la mejor gestión de sus inversiones. Son conocimientos que se estudian en el Grado en ADE online, una titulación que facilita al alumno una visión global del mundo de la empresa y le dota de un perfil profesional multidisciplinar que le prepara para trabajar en empresas, entidades financieras, consultorías, docencia o embarcarse en un propio proyecto empresarial.