Francisco Chicharro López
La medicina, las matemáticas y la computación, entre otras disciplinas, convergen en este fenómeno con diferentes pesos.

Las matemáticas están cada vez más integradas en nuestro día a día. A partir de la revolución tecnológica de finales del siglo XX, que tuvo como efecto la reducción de los costes en la informática, prácticamente en todos los hogares se dispone de un sistema de computación integrado en un ordenador personal.
Es precisamente la computación la que se ha puesto al servicio de la matemática aplicada, integrando múltiples funcionalidades en los diferentes dispositivos electrónicos que utilizamos con frecuencia.
La matemática, al servicio de la ciencia
Un fenómeno que está afectando a los quehaceres diarios de la población es la infección por causa del coronavirus o COVID-19. La medicina, las matemáticas y la computación, entre otras disciplinas, convergen en este fenómeno con diferentes pesos. En este caso, la matemática aplicada y la computación se ponen al servicio de la medicina.
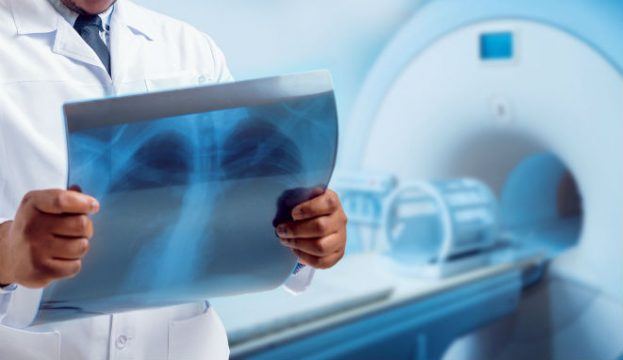
El tratamiento morfológico de la imagen tiene un gran contenido matemático, y se basa en campos como la teoría de conjuntos o la topología. A grandes rasgos, esta disciplina permite discriminar elementos, describir objetos o suprimir ruidos de la imagen capturada.
La tomografía computarizada o TAC consiste en un diagnóstico por imágenes. A partir de la captura con rayos X de imágenes transversales, estas son cargadas en un computador. Con el tratamiento morfológico de la imagen se pueden detectar anomalías de un modo mucho más eficiente que visualizando la imagen en bruto.
Tomografías vitales para el diagnóstico
Los primeros artículos científicos relacionados con tomografías computarizadas de pacientes con el virus COVID-19 no se han hecho esperar. En Dai, y otros, 2020, y Zu, y otros, 2020, se pueden observar una serie de casos de estudio de pacientes de Wuhan infectados. A estos pacientes se les han practicado tomografías pulmonares y de tórax, analizando las afecciones pulmonares causadas por la infección.
Otra de las cuestiones que preocupa a la población es la duración de las medidas que se están tomando para frenar la expansión del virus.
Otra de las cuestiones que preocupa a la población es la duración de las medidas que se están tomando para frenar la expansión del virus. El hashtag #Frenarlacurva (#Flattenthecurve) está teniendo un alto impacto en las redes sociales. De hecho, en The Spinoff se ha publicado un gif que se ha viralizado por cómo de ilustrativo es para la población, marcando como objetivo aplanar la curva del número de infecciones.
Fernando Simón, de @sanidadgob, explica por qué es importante seguir a rajatabla las recomendaciones de los expertos. Debemos implicarnos todos y todas para #FrenarLaCurva.#INFOCoronavirus pic.twitter.com/gQ20mObJUV
— Salud Pública (@SaludPublicaEs) March 11, 2020
El director del Centro de Coordinación de Alertas y Emergencias Sanitarias del Ministerio de Sanidad, Fernando Simón, explica en Twitter la curva de infección epidemiológica. Hace especial énfasis en qué fase de la curva nos encontramos. También, en cómo tomar determinadas acciones, que puede producir que se aplane la curva.
De este modo, el sistema de salud pública podría tener la capacidad suficiente para poder atender a todos los infectados, así como reducir el número de infecciones.
Pero, ¿en qué consiste esta curva? Para ello, tendríamos que recurrir a los modelos de probabilidad; de nuevo, las matemáticas aparecen en nuestro camino.

En El Confidencial han publicado un artículo interesante acerca de un modelo que se está utilizando para predecir el impacto temporal de los infectados por COVID-19. Lejos de las reglas de tres, el profesor Ángel Manuel Ramos del Olmo indica acerca de los modelos exponenciales: “No es que no funcionen nunca, es que pronto dejan de valer”.
Ramos añade que “hay que tener claro que son modelos matemáticos para situaciones complejas y, por tanto, es imposible hacerlos perfectos”, así como que su equipo trabaja con un modelo similar al SIR. En concreto, se puede observar en uno de sus informes técnicos (Ivorra & Ramos, 2020) que utilizan su modelo propio Be-CoDiS.
El modelo SIR
El modelo SIR fue propuesto en (Kermack & McKendrick, 1927). Relaciona en función del tiempo a la población susceptible de ser infectada (S), la población que ya se encuentra infectada (I), y la población que ya está recuperada de la infección (R), siendo la población total (N) que cumple N=S+I+R.
Este modelo asume que la inmunidad completa se confiere por un solo ataque, y que un individuo no es infeccioso en el momento en que recibe la infección. Asimismo, concluye que pequeños aumentos de la tasa de contagio pueden dar lugar a grandes epidemias.

En Wang, y otros, 2020, han optado por un modelo evolucionado del SIR, el SEIR, que dio resultados aceptables en el caso del Ébola en 2004 (Chowell, Hengartnet, Castillo-Chavez, Fenimore, & Hyman, 2004) en el que se incluye a la población infectada pero que no infecta a otros (E), donde ahora N=S+E+I+R.
Este modelo que se utiliza en dicho trabajo es el sistema de cuatro ecuaciones diferenciales

donde β representa la tasa de contagio, σ es la inversa del tiempo promedio de incubación y γ es la inversa del tiempo promedio de infección. Los parámetros β, σ y γ son particulares para cada agente infeccioso, y su valor es clave para predecir el comportamiento de la infección.
La resolución del sistema de ecuaciones diferenciales por métodos numéricos es muy sencilla.
La resolución del sistema de ecuaciones diferenciales por métodos numéricos es muy sencilla. En la simulación que presentamos, vamos a tomar datos completamente ficticios. Tomamos como tasa de contagio β=1/3, como tiempo promedio de incubación 1/σ=6 días y como tiempo promedio de infección 1/γ=18 días.
Como valores iniciales de las variables, tomamos una población de S_0=1 millón de habitantes, y para el resto de valores nos basamos proporcionalmente en (Wang, y otros, 2020), es decir, I_0=4 infectados, E_0=20I_0=80 infectados que no transmiten y R_0=0 recuperados. Utilizamos el método de Runge-Kutta de orden 4 para resolver el sistema de ecuaciones diferenciales a lo largo de 120 días, con un paso de 1 día, y obtenemos los resultados de la figura.

En esta figura no se considera un modelo dinámico de los parámetros, sino que la tasa de contagio toma un valor fijo. Sin embargo, la realidad indica que la tasa de contagio varía entre personas y fechas, en función de las medidas de contención que se tomen.
Situaciones extraordinarias
Tanto en situaciones cotidianas como extraordinarias, las matemáticas se ponen al servicio de la sociedad. En el Grado en Matemática computacional online de UNIR quedan perfectamente reflejados tales aspectos. Asimismo, los alumnos del Máster Universitario en Ingeniería Matemática y Computación de esta Universidad adquieren los conocimientos necesarios -sobre la base de la computación- para modelar y resolver problemas matemáticos y estadísticos que surgen en los ámbitos científicos (como el expuesto en este artículo) tecnológicos, industriales y sociales.
De todas formas, aprender a modelar fenómenos de la humanidad es hartamente complicado, pero hay equipos de trabajo que consiguen ajustar sus modelos con unos errores aceptables. Lo que podemos hacer como población, más que predecir qué va a ocurrir, es aplanar la curva, para lo cual necesitamos un alto grado de responsabilidad.
Este artículo fue elaborado en coautoría con Daniel Pérez Palau






